티스토리 뷰
문제
코딩테스트 연습 - 트리 트리오 중간값
5 [[1,5],[2,5],[3,5],[4,5]] 2
programmers.co.kr
풀이
- 임의의 노드 1로부터 가장 먼 노드 A를 찾는다.
- A로부터 각 노드까지의 거리를 찾는다
- 이 때 가장 먼 거리의 노드가 여러개라면 A노드와 먼 노드 중 2개를 선택하면 되므로 가장 먼 거리 리턴
- 가장 먼 거리의 노드가 B 하나라면 다시 B 를 기준으로 탐색
- B로부터 각 노드까지의 거리를 찾는다
- 이 때 역시 가장 먼 거리의 노드가 여러개라면 B노드와 먼 노드 중 2개를 선택하면 되므로 가장 먼 거리 리턴
- 가장 먼 거리의 노드가 A 하나라면 A와 B의 거리(트리의 지름)-1을 리턴
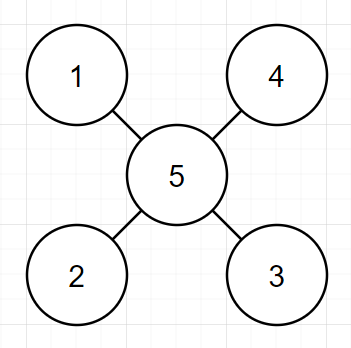
위와 같은 입력의 경우 2-1에서 리턴이 된다.
노드 1에서 가장 먼 노드는 3이고, 3은 1,2,4 중 두개를 고르면 가장 큰 값이 되기 때문이다!

이런 입력의 경우는 3-2에서 리턴이 된다.
처음 1을 기준으로 찾으면 A는 4, B는 다시 1이 되면서 트리의 지름을 찾고 [1,2,4], [1,3,4] 등이 답이 되어 트리의 지름-1이 정답이 된다.
하지만 이 경우에서는 3번을 수행하지 않고 2번까지 한 다음 지름-1을 리턴해도 되는데 왜 3번 과정을 한번 더 해줘야할까?!

위와 같은 경우, 처음 1을 기준으로 가장 먼 노드를 찾으면 5가 된다.
이제 노드 5번을 기준으로 다시 거리를 탐색하면 8번 노드가 가장 먼 노드가 된다.
만약 여기서 2번까지만 수행하고 함수를 종료하면 현재 가장 먼 노드의 갯수는 1개이므로 오답인 트리의 지름-1이 리턴될 것이다.
다시 8번을 기준으로 가장 먼 노드를 찾으면 5,6번 노드 두개를 발견하게 되므로 최대 길이인 트리의 지름을 제대로 정답으로 찾아 리턴할 수 있다~!~!!!~!
코드
static public int solution(int n, int[][] edges) {
List<Integer>[] list = new ArrayList[n+1];
for(int i=1; i<=n; i++) list[i] = new ArrayList<Integer>();
for(int[] edge : edges) {
list[edge[0]].add(edge[1]);
list[edge[1]].add(edge[0]);
}
// 임의의 점 1에서 가장 먼 노드 X를 찾음 (start)
int start = 1, cnt = 0;
int[] result = bfs(list, start, n);
for(int i=2; i<=n; i++)
if(result[i]>result[start]) start = i;
// X에서 각 노드까지의 값을 찾음
cnt = 0;
result = bfs(list, start, n);
for(int i=1; i<=n; i++)
if(result[i]>result[start]) start = i;
for(int i=1; i<=n; i++) if(result[start]==result[i]) cnt++;
if(cnt>=2) return result[start]; // 만약 가장 먼 노드가 2개라면 X와 이 두 노드를 선택하면 되므로 리턴
// X에서 가장 먼 노드인 Y를 기준으로 각 노드까지의 값을 찾음
cnt = 0;
result = bfs(list, start, n);
for(int i=1; i<=n; i++) if(result[start]==result[i]) cnt++;
if(cnt>=2) return result[start];
return result[start]-1;
}
static int[] bfs(List<Integer>[] list, int start, int n) {
boolean[] visit = new boolean[n+1];
int[] dist = new int[n+1];
Queue<Integer> queue = new LinkedList<Integer>();
queue.add(start);
visit[start] = true;
while (!queue.isEmpty()) {
int now = queue.poll();
for(int i : list[now]) {
if(visit[i]) continue;
visit[i] = true;
queue.add(i);
dist[i] = dist[now] + 1;
}
}
return dist;
}'Algorithm' 카테고리의 다른 글
| [Algorithm] 백준 1197 최소스패닝트리 - union-find, 크루스칼 알고리즘 (0) | 2020.10.24 |
|---|---|
| [Algorithm] Union-Find의 개념과 구현 (0) | 2020.10.24 |
| [Algorithm] 백준 1167 트리의 지름 (0) | 2020.10.12 |
| [Algorithm] 백준 5577 회전초밥 - 슬라이딩윈도우 (0) | 2020.09.09 |
| [Algorithm] 2019 카카오 인턴십 - 튜플 (Map 정렬하기) (0) | 2020.08.29 |
