티스토리 뷰
Maze
- 아래와 같은 구조의 미로를 나가는 길을 찾는 것이 목표
- 흰색은 지날 수 있는 길이며, 파란색은 막혀있는 벽
- 입구는 [0][0]이며 출구는 [N-1][N-1]

구현
-
무한 루프에 빠지지 않으려면 반드시 base case로 수렴해야함
-
이 경우에서는 이미 방문한 cell을 표시하여 무한 반복을 해결
public class Maze {
/*
* 현재 위치에서 출구까지 가는 경로가 있으려면
* 1) 현재 위치가 출구이거나 (base case)
* 2) 이웃한 4개의 cell들 중 하나에서 현재 위치를 지나지 않고 출구까지 가는 경로가 있거나 (recursive)
*/
private static int N = 8;
private static int [][] maze = {
{0, 0, 0, 0, 0, 0, 0, 1},
{0, 1, 1, 0, 1, 1, 0, 1},
{0, 0, 0, 1, 0, 0, 0, 1},
{0, 1, 0, 0, 1, 1, 0, 0},
{0, 1, 1, 1, 0, 0, 1, 1},
{0, 1, 0, 0, 0, 1, 0, 1},
{0, 0, 0, 1, 0, 0, 0, 1},
{0, 1, 1, 1, 0, 1, 0, 0}
};
private static final int PATHWAY_COLOUR = 0; //지나갈 수 있는 통로
private static final int WALL_COLOUR = 1; //지나갈 수 없는 벽
private static final int BLOCKED_COLOUR = 2; //탐색 결과 해답 통로가 아닌 경우
private static final int PATH_COLOUR = 3; //탐색 결과 해답 통로인 경우
public static boolean findMazePath(int x, int y) { //경로를 탐색하는 함수
if (x<0 || y<0 || x>=N || y>=N) { //현재 좌표가 유효한 위치가 아닌 경우
return false;
} else if (maze[x][y] != PATHWAY_COLOUR) { //현재 좌표가 탐색이 필요 없는 경우
return false;
} else if (x==N-1 && y==N-1) { //현재 좌표가 출구인 경우
maze[x][y] = PATH_COLOUR;
return true;
} else { //위의 세 경우가 아닐 경우 경로 탐색
maze[x][y]= PATH_COLOUR; //방문 표시
if (findMazePath(x-1, y) || findMazePath(x, y+1) //인접한 4개의 cell에 대하여 recusive 함수 호출
|| findMazePath(x+1, y) || findMazePath(x, y-1))
return true; //위의 네개의 경우 중 하나라도 true일 시 true 리턴
}
maze[x][y] = BLOCKED_COLOUR;
return false;
}
public static void printMaze() {
for(int x=0; x<N; x++) {
System.out.print("{");
for(int y=0; y<N; y++) {
if(y < N-1)
System.out.print(maze[x][y] + ", ");
else
System.out.print(maze[x][y]);
}
System.out.println("}");
}
}
public static void main(String [] args) {
findMazePath(0, 0);
printMaze();
}
}
Blob count
- blob에 포함된 image pixel의 갯수를 출력하는 것이 목표
- blob이 아닐 경우(background pixel일 경우) 0 출력

구현
- 무한 루프에 빠지지 않기 위해 이미 blob의 크기를 구한 pixel은 2로 표시
- 현재 pixel의 인접한 8개 pixel의 blob의 크기를 구하면 현재 pixel의 blob의 크기도 구할 수 있음
public class Recursion_blob {
/*
* blob의 크기를 구하려면
* 1) image pixel이 아닐 경우 0 출력
* 2) image pixel일 경우 북,북동,동,동남,남,남서,서,북서 8개의 픽셀이 포함된 blob의 크기를 구하여 +1
*/
private static int BACKGROUND_COLOR = 0; //image pixel이 아닌 경우
private static int IMAGE_COLOR = 1; //image pixel인 경우
private static int ALREADY_COUNTED = 2; //이미 blob의 크기를 계산한 pixel인 경우
private static int N = 8;
private static int[][] grid = {
{1, 0, 0, 0, 0, 0, 0, 1},
{0, 1, 1, 0, 0, 1, 0, 0},
{1, 1, 0, 0, 1, 0, 1, 0},
{0, 0, 0, 0, 0, 1, 0, 0},
{0, 1, 0, 1, 0, 1, 0, 0},
{0, 1, 0, 1, 0, 1, 0, 0},
{1, 0, 0, 0, 1, 0, 0, 1},
{0, 1, 1, 0, 0, 1, 1, 1},
};
public static int countCells(int x, int y) {
if(x<0 || x>=N || y<0 || y>=N) //구하려는 pixel의 좌표가 유효하지 않은 경우
return 0;
else if (grid[x][y] != IMAGE_COLOR) //구하려는 pixel이 image pixel이 아니거나 이미 탐색한 경우
return 0;
else { //위의 두 경우가 아닌 경우 탐색 시작
grid[x][y] = ALREADY_COUNTED; //count한 pixel로 표시
//현재 pixel에 인접한 8개의 pixel이 포함된 blob의 크기를 구하여 더한 값이 결과
return 1 + countCells(x-1, y) + countCells(x-1, y+1) + countCells(x, y+1) +
countCells(x+1, y+1) + countCells(x+1, y) + countCells(x+1, y-1) +
countCells(x, y-1) + countCells(x-1, y+1);
}
}
public static void printGrid() {
for(int x=0; x<N; x++) {
System.out.print("{");
for(int y=0; y<N; y++) {
if(y < N-1)
System.out.print(grid[x][y] + ", ");
else
System.out.print(grid[x][y]);
}
System.out.println("}");
}
}
public static void main(String [] args) {
System.out.println("result : " + countCells(0,0));
printGrid();
}
}
N-queens
- 그림처럼 NxN크기의 체스 보드에 N개의 말을 놓는 것이 목표
- 동일한 행, 동일한 열, 동일한 대각선 상에 말이 놓이면 안되는 것이 조건

Back tracking
- 상태 공간 트리를 깊이 우선 방식으로 탐색하여 해를 찾는 알고리즘
- 주어진 조건에 맞춰 차례대로 수행하다가, 조건에 부합하는 경우가 없는 경우 가장 최근의 결정을 번복하여 모든 경우의 수를 탐색
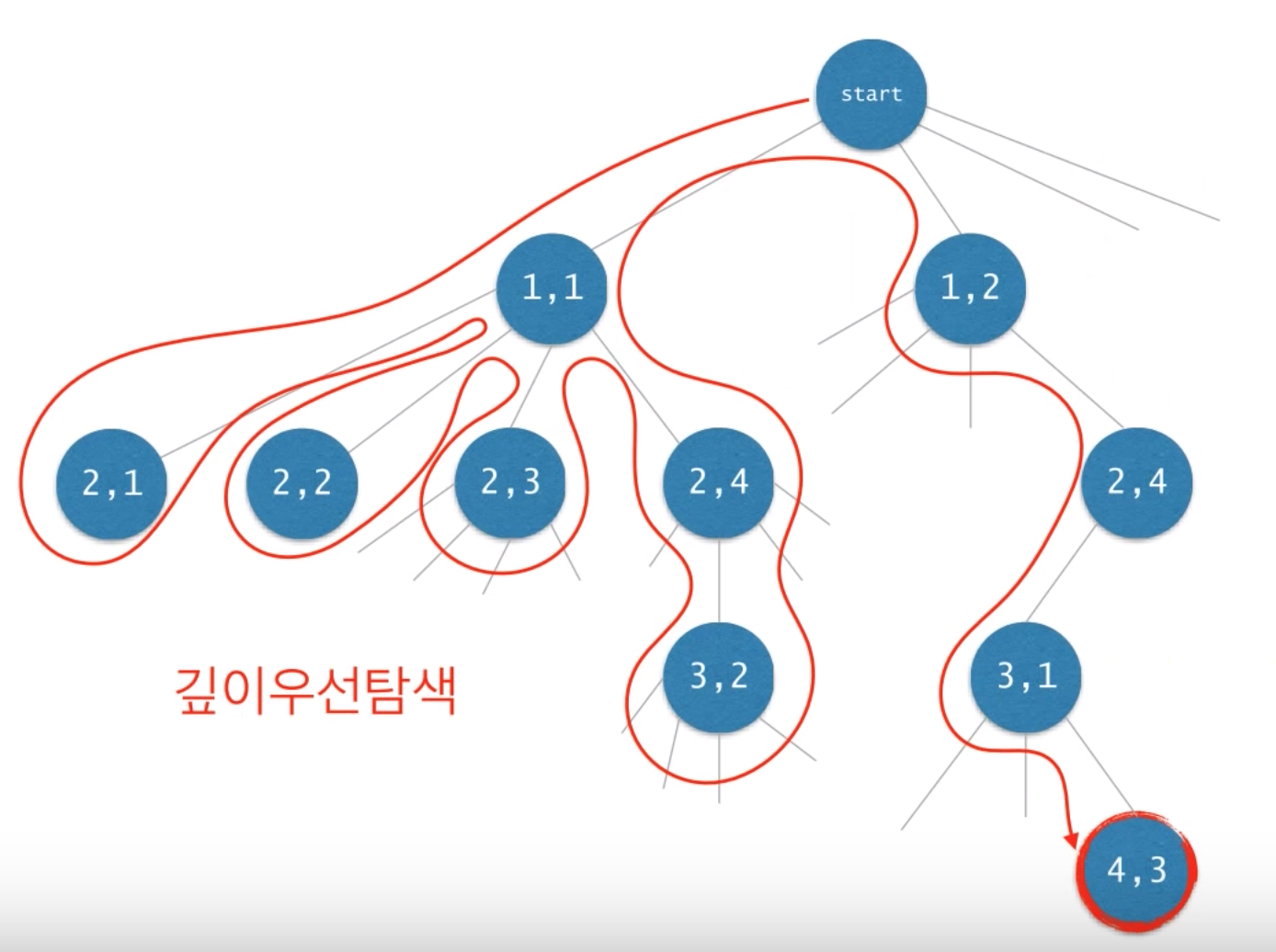
- back tracking을 구현하는 일반적인 방식
return-type queens(arguments) { //매개변수는 상태 공간 트리에서 현재 위치한 노드
if non-promising //더 이상 탐색할 필요가 없는 경우 (non-promising)
report failure and return;
else if success //해답을 찾은 경우
report answer and return;
else
visit children recursively; //자식 노드를 recursive하게 탐색
}
구현
- 매개변수 level : 현재 노드의 level을 의미
- 전역변수 cols : i번에서 level번째 말이 어느 열에 놓였는지 의미 (cols[i] = j인 경우 말이 (i행, j열)에 위치)
- 첫 시작은 queens(0)
public class Recursive_NQueens {
/*
* 모든 조건을 만족하는 방법을 찾으려면
* 1) level(행)번째 말들을 차례대로 모든 위치에 놓아보고
* 2) 조건에 부합하지 않는 경우 바로 직전에 움직인 말의 위치 수정
*/
private final static int N = 8;
private static int [] cols = new int[N+1];
private static boolean queens(int level) {
if(!promising(level)) //더 이상 다음 경우를 탐색 할 필요가 없는 경우(해당 자리에 놓으면 안되는 경우)
return false;
else if(level == N) { //첫번째 if문을 통과하였으며, 모든 말이 다 놓인 경우
for (int i = 1; i <= N; i++)
System.out.println("(" + i + ", " + cols[i] + ")");
return true;
}
//첫번째 if문을 통과하였으므로 현재 level의 말의 위치는 놓아도 되는 자리
//밑의 for문은 자식 노드를 recursive하게 방문
for(int i=1; i <=N; i++) { //1번부터 N번째 열까지 놓아보는 반복문
cols[level + 1] = i; //level+1번째 말을 (level+1행,i열)의 위치에 놓겠다는 뜻
if(queens(level+1)) //(level+1행,i열)의 위치가 유효한지 검사하기 위해 함수 호출
return true; //다음 말이 놓이면 true 반환하여 반복문을 나옴
}
return false; //해결 가능한 방법이 없음
}
/*
* 다음 경로를 탐색할 필요가 없는 경우
* 1) 이전 말들과 비교하여 같은 열에 놓인 경우
* 2) 이전 말들과 비교하여 대각선 상에 놓인 경우
*/
private static boolean promising(int level) { //다음 경우를 탐색할 필요가 있는지 검사하는 함수
for(int i=1; i<level; i++) { //이전 level에 놓인 말들과 조건 검사 수
if(cols[i] == cols[level]) //같은 열에 놓인 경우
return false;
else if((level - i) == Math.abs(cols[level] - cols[i])) //대각선 상에 놓인 경우
return false;
}
return true; //같은 열 또는 대각선 상에 놓이지 않았다면 true 반환
}
public static void main(String[] args) {
queens(0);
}
}
power set (멱집합)
- 멱집합 : 어떤 집합의 모든 부분집합
- 원소가 n개인 집합의 모든 부분집합의 개수는 2ⁿ개
상태 공간 트리
- 해를 찾기 위해 필요한 모든 경우의 수가 나열되어 있는 트리
- include 와 exclude가 반대로 써있음 (오타)

구현
- {a, b, c, d, e, f} 의 모든 부분집합
- 원소 a를 포함하지 않는 부분집합 = {b, c, d, e, f}의 모든 부분집합
- 원소 a를 포함하는 부분집합 = {b, c, d, e, f}의 모든 부분집합에 {a}를 추가한 집합들
- {b, c, d, e, f}의 모든 부분집합에 {a}를 추가한 집합들
- 원소 b를 포함하지 않는 부분집합 = {c, d, e, f}의 모든 부분집합들에 {a}를 추가한 집합들
- 원소 b를 포함하는 부분집합 = {c, d, e, f}의 모든 부분집합들에 {a, b}를 추가한 집합들
- {c, d, e, f}의 모든 부분집합들에 {a}를 추가한 집합들
- 원소 c를 포함하지 않는 부분집합 = {d, e, f}의 모든 부분집합들에 {a}를 추가한 집합들
- 원소 c를 포함하는 부분집합 = {d, e, f}의 모든 부분집합들에 {a, c}를 추가한 집합들
- base case에 도달할 때 까지 위의 과정을 반복해 구한 모든 부분집합을 출력
public class Recursion_powerSet {
private static char data[] = {'a','b','c','d','e','f'};
private static int n = data.length; //위의 배열의 경우 n=6
private static boolean [] include = new boolean [n]; //크기가 6인 boolean 값을 가진 배열
public static void powerSet(int k) { //k는 배열의 index
//상태공간트리 상에서 현재위치가 리프노드
if(k==n) { //base case
for (int i=0; i<n; i++) //배열의 모든 원소 출력
if (include[i])
System.out.print(data[i] + " ");
System.out.println();
System.out.println("if문 완료");
return;
}
//리프노드의 위치가 아니라면,
//data k를 포함하지 않는 경우 (트리상에서 왼쪽 노드)
include[k] = false; //k를 포함하지 않는다는 표시
powerSet(k+1);
//data k를 포함하지 않는 경우 (트리상에서 오른쪽 노드)
include[k] = true; //k를 포함한다는 표시
powerSet(k+1);
}
public static void main(String[] args) {
powerSet(0);
}
}'Algorithm' 카테고리의 다른 글
| [Algorithm] 그래프 Graph - 개념과 표현 (0) | 2020.04.08 |
|---|---|
| [Algorithm] 정렬 Sort - Counting sort, Radix sort (0) | 2020.04.05 |
| [Algorithm] 정렬 Sort - Heap sort (0) | 2020.04.03 |
| [Algorithm] 정렬 Sort - Merge sort, Quick sort (0) | 2020.04.01 |
| [Algorithm] 정렬 Sort - Selection sort , Bubble sort , Insertion sort (0) | 2020.03.31 |
